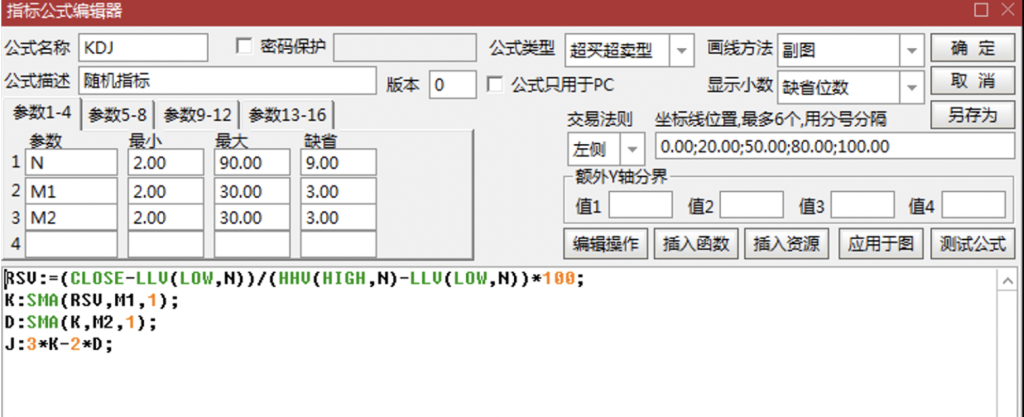
熟悉量化的朋友估计都看过指标公式编辑器,国内比较具有代表性的就是通达信的公式编辑器了,如下图所示:
下面这个是国外 TradeView 的 Pine Editor,都提供了在线编写代码的功能:
公式编辑器的模式极大的提高了指标定制的灵活度,并且极大的降低了客户学习使用成本,已成为现在各种量化平台首选技术方案。有同学要问了,搞这么复杂做啥,我把指标算法写死在代码里,把省下来的时间拿去摸鱼不是更好吗?好像有点道理,我们还是先来看看使用场景吧。
使用场景分析
公式编辑器其实就是一个代码编译器,提供了在线编写代码,解析编译代码的功能,并且安全可控。有以下场景需要用到
- K线图表指标在线定制,绘图定制等
- 选股器定制
- 策略编辑器
- 代码编辑器
- 发明新的程序开发语言
那么开发一个指标公式编辑器需要用到什么算法呢?
递归下降算法
对这个算法有所了解的同学都知道,递归下降算法通常用于编译器、解释器和正则表达式引擎中,以分析语法结构。通过对输入流的逐个字符分析,分解成一个一个的语法单元,一个语法单元可能是整形,浮点型数值或者函数或者表达式等,数值单元直接返回数值,单元即无需递归,函数表达式则继续按照算法递归,直到解析成最小语法单元无法分解为止,此时结束递归并返回数据。这是一个大致的算法原理,具体生产中会更复杂一点。
流程图
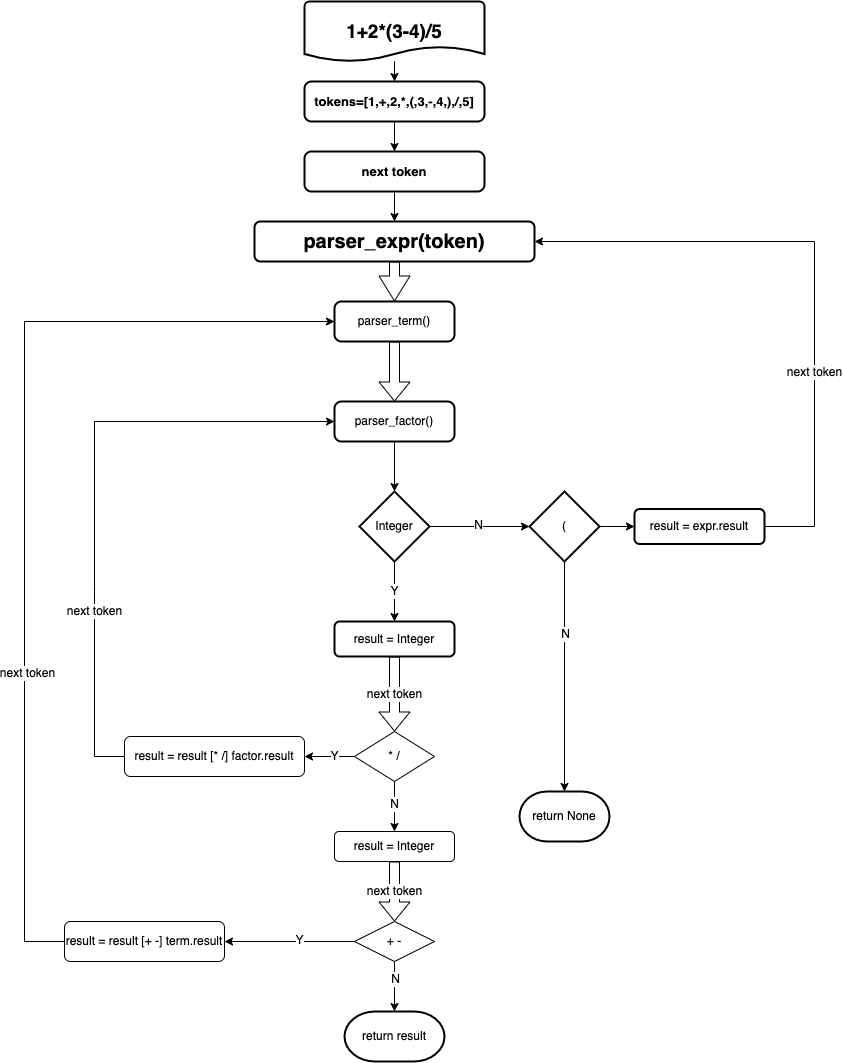
下面是一个解析算数表达式 1+2*(3-4)/5 的流程图:
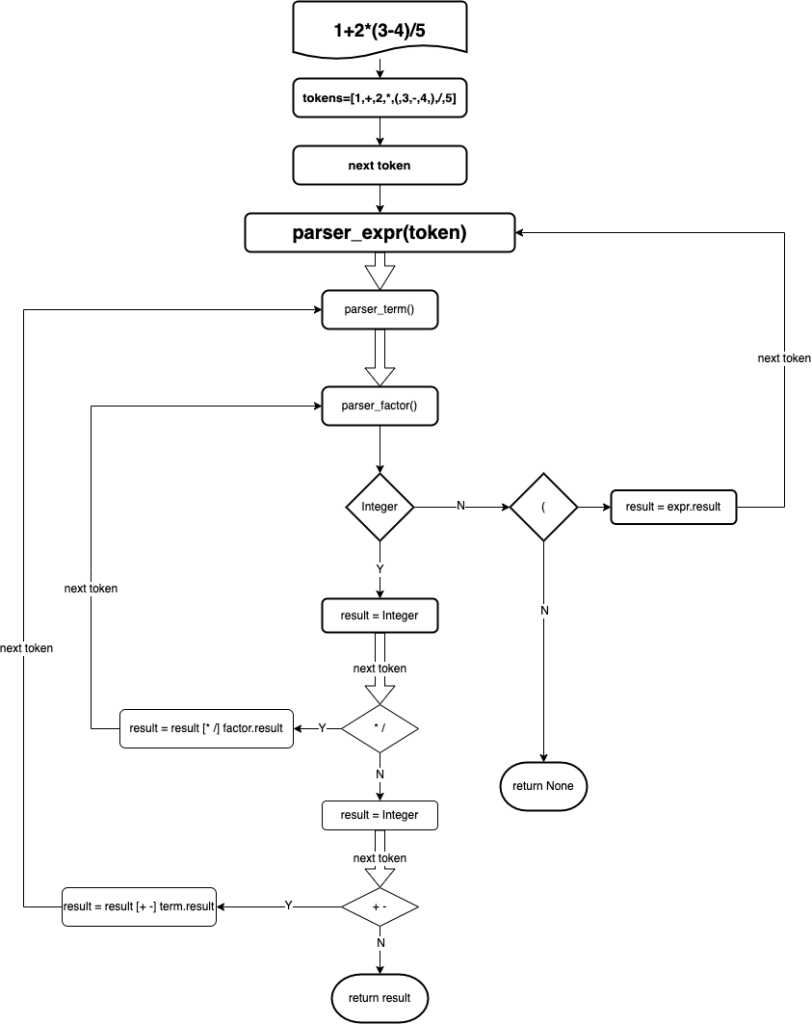
在往下看之前我们需要先了解两个名次概念
词法分析器
Lexer :负责解析输入流的每个字符属于什么类型,打上标签 TOKEN
语法解析器
Parser :负责解析每个TOKEN的的运算逻辑,例如数字返回数值,加减乘除执行算数运算等。
代码实现
# 语法解析器
class Parser:
def __init__(self, lexer:Lexer):
# 传入词法解析器,把表达式转换为Token集合
self.lexer = lexer
# 这里相当于取得第一个词法解析器的Token
self.current_token = self.lexer.get_next_token()
def parse(self):
return self.expr()
# 表达式字符串 递归开始
def expr(self):
# 处理项
result = self.term()
# 处理加减
while self.current_token.type in (TokenType.PLUS, TokenType.MINUS):
op = self.current_token
self.eat(op.type)
# 处理加减符号右边项
term = self.term()
if op.type == TokenType.PLUS:
result = result + term
elif op.type == TokenType.MINUS:
result = result - term
return result
# 项
def term(self):
# 处理因子
result = self.factor()
# 处理乘除,因为先乘除后加减,乘除符号连接成一个因子处理
while self.current_token.type in (TokenType.MUL, TokenType.DIV):
op = self.current_token
self.eat(op.type)
# 处理乘除号右边因子
factor = self.factor()
if op.type == TokenType.MUL:
result = result * factor
elif op.type == TokenType.DIV:
result = result / factor
return result
# 处理因子
def factor(self):
token = self.current_token
# 处理整形数字,直接返回整形结果
if token.type == TokenType.INTEGER:
self.eat(TokenType.INTEGER)
return int(token.value)
# 处理左括号,进入括号继续递归解析表达式
elif token.type == TokenType.LPAREN:
self.eat(TokenType.LPAREN)
result = self.expr()
self.eat(TokenType.RPAREN)
return result
# 继续下一个
def eat(self, token_type):
if self.current_token.type == token_type:
self.current_token = self.lexer.get_next_token()
else:
raise Exception('Syntax error')计算结果
from src.tokenizer import Lexer
from src.parser import Parser
if __name__=="__main__":
expressions = """
1+2*(3-4)/5
"""
# 词法分析器
lexer = Lexer(expressions)
# 语法解析器
parser = Parser(lexer)
# 解析并返回结果
result = parser.parse()
print(result) # Output: 0.6可以看到,经过递归解析,最终得到了准确的计算结果 1+2*(3-4)/5=0.6
有同学说了,你这个解析器太简单了,只能加减乘除,如果表达式有变量有函数呢,如果有多条表达式呢?这个同学问的很好,就像mask说过的,任何复杂问题都能分成若干小的问题单元,逐个解决问题单元,整个复杂问题即可迎刃而解,接下来我们会提出更复杂的问题表达式。
就让我们像 JamesGosling(Java之父)、Guido van Rossum(Python之父)、Rasmus Lerdorf(PHP之父)、Dennis MacAlistair Ritchie(C语言之父)等等等大神一样思考吧!
让鸡血流遍你的身体,爆肝吧!!!!
复杂公式语句
因为整个篇幅是讲量化相关,那么我们先来看一个指标公式吧,例如 KDJ 公式,这个相对复杂一点了吧,有变量赋值,有函数,有算数运算,有多条语句等。
咱们先来解决这样的问题吧
KDJ 公式
N:=9; M1:=3; M2:=3;
RSV:=(CLOSE-LLV(LOW,N))/(HHV(HIGH,N)-LLV(LOW,N))*100;
K:=SMA(RSV,M1,1);
D:=SMA(K,M2,1);
J:=3*K-2*D;面对复杂问题,我们第一步就要分解问题,把KDJ公式进行分解如下
- 变量 例如 N
- 赋值符号 例如 :=
- 括号表达式 例如 ((…))
- 函数 例如 LLV(LOW,N)
- 算数符号 例如 +-*/
- 结束符 例如 ;
似乎只要我们能解决以上六个问题单元,我们就能解决KDJ公式解析问题。有想法那就要行动起来,爆肝开始了….
解决变量赋值问题
正则识别
我们定义变量是由字母开头和字母数字下划线组合而成,那么我们定个正则来识别变量名。
# 一些正则
class RegRolues:
# 识别变量名称正则
VARIABLE = r'^[a-zA-Z_][a-zA-Z0-9_]*$'词法分析
因为第一步需要对输入流进行词法分析,也就是给每个字符打标签,所以要在词法分析器中增加变量识别标识 (我们需要给每个字符打上标识 TOKEN,便于给语法解析器处理)。因为对于变量来说,在等号左边的时候是赋值,在等号右边的时候是取值,所以我们要给标识加一个方向属性,指示这个TOKEN是在等号左边还是右边。
# 在词法分析器 Lexer->get_next_token() 中加入赋值符号,换行符,变量识别逻辑
# 赋值符号
if self.current_char == ':':
self.advance()
if self.current_char == '=':
self.advance()
# 进入等号右边
self.direction = Direction.RIGHT
return Token(TokenType.EQUAL, ':=',self.direction)
# 换行符
if self.current_char == ';':
# 进入等号左边
self.advance()
self.direction = Direction.LEFT
return Token(TokenType.NEWLINE, '=',self.direction)
# 变量
if re.match(configer.RegRolues.VARIABLE, self.current_char):
# 设别变量
return self.variable()语法分析
我们在之前的算数表达式基础上加上变量因子处理,跟处理整型因子是一样的逻辑,只是要解决未来某个时刻赋值取值的问题。所以我们要设计一个缓存空间,专门用来存储变量地址,变量值等。
# 在语法分析器的因子函数中 Parser->factor() 加入变量缓存逻辑
self.eat(TokenType.VARIABLE)
# 如果是在等号左边,缓存变量
var_name = str(token.value)
result = None
if token.direction==Direction.LEFT:
# 缓存变量并初始化为None
self.caches[var_name] = None
result = var_name
else:
# 如果在等号右边,表示取值
if var_name in self.caches.keys():
var_value = self.caches.get(var_name)
result = var_value
else:
# 是系统变量属性值
if hasattr(self,var_name):
result = getattr(self,var_name)
return result在项处理中加入赋值符号的处理
# 在语法分析器 Parser 的项函数 term() 中加入赋值符号的处理
if self.current_token.type == TokenType.EQUAL:
# 需要解析赋值符号右边的表达式的值赋值给左边的变量
op = self.current_token
self.eat(op.type)
# 处理等号右边的表达式
result = self.expr()
# 取出等号左边的变量名
var_name,var_value = self.caches.popitem()
# 赋值变量
self.caches[var_name] = result
return result调试解析变量
这样我们就完成了变量的逻辑处理,来看看自己的小小成绩吧,我们调试一下
expressions = """
N:=9; M1:=3; M2:=3;
RSV:=(CLOSE-LLV(LOW,N))/(HHV(HIGH,N)-LLV(LOW,N))*100;
K:=SMA(RSV,M1,1);
D:=SMA(K,M2,1);
J:=3*K-2*D;
"""
try:
# 词法分析器
lexer = Lexer(expressions)
# 语法解析器
parser = Parser(lexer)
# 解析并返回结果
result = parser.parse()
print(result) # Output: 0.6
except Exception as e:
traceback.print_exc()可以看到打印输出了TOKEN分析结果
Token(VARIABLE, 'N')
Token(EQUAL, ':=')
Token(INTEGER, 9)
Token(NEWLINE, ';')
9在我们的缓存空间中也赋值了N变量的值
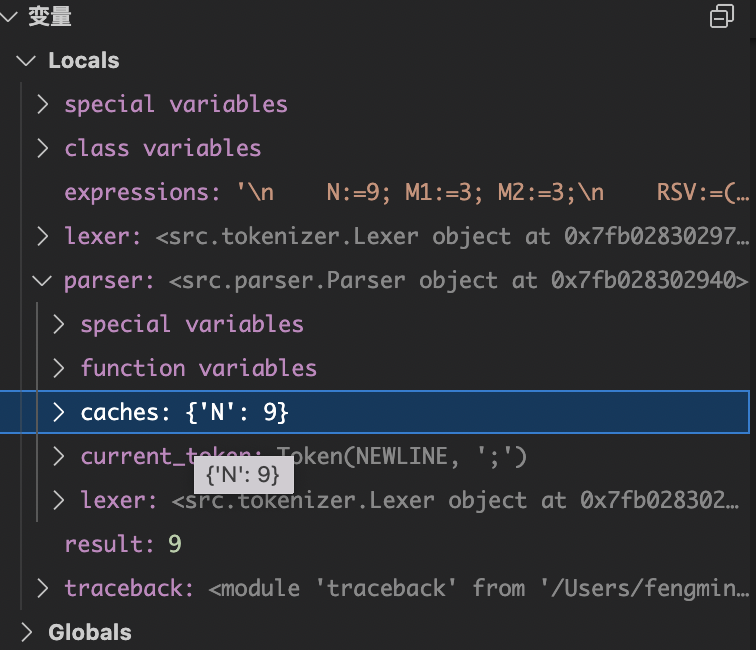
上面即完了第一条语句的解析工作,按照这样的逻辑处理每条语句即可。
解决括号表达式问题
递归到括号后,需要把括号后面的语句当作表达式进行解析,并取得解析返回值。
self.eat(TokenType.LPAREN)
# 解析括号后面表达式,遇到右括号会自动停止递归并返回值
result = self.expr()
self.eat(TokenType.RPAREN)
return result解决函数解析问题
函数解析相对来说复杂很多,在实际生产中随着业务的扩张会更复杂,但是万变不离其宗。函数也是由表达式组成,既然都是表达式,那么解析的逻辑都是一样的。
首先我们需要思考几个问题
- 公式中的函数从哪里来的?
既然是你允许调用函数,那么实现函数当然由你来做,不然呢。所以首先你需要自己在系统中实现函数的功能。 - 函数有多个参数,如何传值呢?
这里我们需要对函数参数进行逐个解析,因为参数有可能是变量、数值,也有可能是表达式方式,但是都不要紧,这些我们前面都已经实现了解析逻辑,按需调用解析方法即可。 - 解析完函数后如何调用呢?
这里需要用到反射了,通过反射获得函数名对应系统方法的句柄,然后通过元组传参的方式即可实现函数执行调用并获得函数返回值。method=getattr(self,函数名) method(*args)
为了实现函数解析功能,我们需要在词法分析器 Lexer、语法分析器 Parser 上分别加上对于的解析逻辑。
函数打好标签
在词法分析器中打好函数标签
# 提取变量名
def variable(self):
# 遇到等号和换行符必须退出
result = ''
while self.current_char is not None and self.current_char!=TokenType.NEWLINE and self.current_char!=":" and self.current_char!="\n":
if re.match(RegRolues.VARIABLE_NAME,self.current_char):
result += self.current_char
else:
# 遇到左括号表明是函数
if self.current_char=="(":
return self.functions(result)
else:
break
self.advance()
return Token(TokenType.VARIABLE, result,self.direction)
# 提取函数表达式
def functions(self,result):
# 提取函数括号内所有字符
i = 0
while self.current_char is not None and self.current_char!=TokenType.NEWLINE and self.current_char!="\n":
result += self.current_char
if self.current_char=="(": i+=1
if self.current_char==")":
i -= 1
if i<=0:
self.advance()
break
self.advance()
return Token(TokenType.FUNCTION, result,self.direction)函数功能实现
需要在系统中实现公式中的函数,这里在解析器里面直接实现。
# 实现属性变量
# 这里是模拟,具体生产自己实现
@property
def LOW(self):
return 10
@property
def HIGH(self):
return 20
@property
def CLOSE(self):
return 30
# 实现公式的函数
def LLV(self,X,N):
# 这里假设实现一个简单的算法
return X * N
# 实现公式的函数
def HHV(self,X,N):
# 这里假设实现一个简单的算法
return X / N
# 实现公式的函数
def SMA(self,X,N,M):
# 这里假设实现一个简单的算法
return X + N + M实现函数解析编译
根据词法分析出来的函数表达式,提取函数名,函数参数组合分别解析,函数参数值可从缓存或系统属性中读取,最后执行函数并取得返回值。
# 处理函数解析逻辑
self.eat(TokenType.FUNCTION)
functions:str = token.value
# 解析函数名和参数
func_name = functions.split("(")[0]
func_params = functions[len(func_name)+1:-1]
# 解析每个参数
args = []
for param in func_params.split(","):
# 这里直接从缓存中获取变量值即可
if param in self.caches.keys():
pval = self.caches.get(param)
args.append(pval)
# 缓存中没有,从系统变量属性中查找
elif hasattr(self,param):
pval = getattr(self,param)
args.append(pval)
else:
args.append(pval)
# 寻找系统函数并执行函数
if hasattr(self,func_name):
method = getattr(self,func_name)
result = method(*args)
return result最终调试
问题都解决后最终调试代码
import traceback
from src.tokenizer import Lexer
from src.parser import Parser
if __name__=="__main__":
expressions = """
1+2*(3-4)/5
"""
expressions = """
N:=9; M1:=3; M2:=3;
RSV:=(CLOSE-LLV(LOW,N))/(HHV(HIGH,N)-LLV(LOW,N))*100;
K:=SMA(RSV,M1,1);
D:=SMA(K,M2,1);
J:=3*K-2*D;
"""
try:
# 词法分析器
lexer = Lexer(expressions)
# 语法解析器
parser = Parser(lexer)
# 解析并返回结果
result = parser.parse()
print(parser.caches) # Output: 0.6
# CLOSE=30,LLV(10,9)=90,HHV(20,9)=2.22,LLV(10,9)=90
# RSV = (30-90)/(2.22-90) * 100 = 68.354
except Exception as e:
traceback.print_exc()输出
Token(VARIABLE, 'N')
Token(EQUAL, ':=')
Token(INTEGER, 9)
Token(NEWLINE, ';')
Token(VARIABLE, 'M1')
Token(EQUAL, ':=')
Token(INTEGER, 3)
Token(NEWLINE, ';')
Token(VARIABLE, 'M2')
Token(EQUAL, ':=')
Token(INTEGER, 3)
Token(NEWLINE, ';')
Token(VARIABLE, 'RSV')
Token(EQUAL, ':=')
Token(LPAREN, '(')
Token(VARIABLE, 'CLOSE')
Token(MINUS, '-')
Token(FUNCTION, 'LLV(LOW,N)')
Token(RPAREN, ')')
Token(DIV, '/')
Token(LPAREN, '(')
Token(FUNCTION, 'HHV(HIGH,N)')
Token(MINUS, '-')
Token(FUNCTION, 'LLV(LOW,N)')
Token(RPAREN, ')')
Token(MUL, '*')
Token(INTEGER, 100)
Token(NEWLINE, ';')
Token(VARIABLE, 'K')
Token(EQUAL, ':=')
Token(FUNCTION, 'SMA(RSV,M1,1)')
Token(NEWLINE, ';')
Token(VARIABLE, 'D')
Token(EQUAL, ':=')
Token(FUNCTION, 'SMA(K,M2,1)')
Token(NEWLINE, ';')
Token(VARIABLE, 'J')
Token(EQUAL, ':=')
Token(INTEGER, 3)
Token(MUL, '*')
Token(VARIABLE, 'K')
Token(MINUS, '-')
Token(INTEGER, 2)
Token(MUL, '*')
Token(VARIABLE, 'D')
Token(NEWLINE, ';')
Token(EOF, None)
{'N': 9, 'M1': 3, 'M2': 3, 'RSV': 68.35443037974684,
'K': 74.35443037974684, 'D': 80.35443037974684, 'J': 223.06329113924053}完美运行!!!
至此,整个大问题都基本得到了“圆满”解决,大问题变小,小问题变无,这就是解决问题的方法了,当然了这也是编译器的基本原理,能耐心看完的应该都能看懂了。
对于函数解析模块,还是有点小问题,是什么呢?不知道大家发现没有,如果函数里面有表达式呢,上面的方法显然处理不来,这里就留个小作业给大家解决了,别光看哦,动起手来吧!
还有就是有兴趣的朋友可以真正实现 LLV,HHV,SMA等函数功能,真正的计算出真实的KDJ数据。
递归下降算法虽然简单易懂,但是也存在缺陷就是它的性能瓶颈,有没有什么好的优化方式呢?或者其他效率更高的算法代替呢?欢迎各位同学提供参考建议。
资料
从中大家能得到什么启发呢,开发一款自己的编程语言如何?一款像Python之父那样、C语言之父那样创造出流行于世界的编程语言,只要足够闲,我相信您一定可以的。
完整的代码在Github上有开源,https://github.com/dsxkline/dsx_base_algorithm
写完这个指标公式编辑器框架,后面我会开源出来,请大家多多指点,多多支持!
觉得可以,点赞收藏转发吧!感谢您的阅读!
2023年3月7日 by dsxquant